Les logarithmes, à quoi ça sert ?

Les logarithmes sont des fonctions mathématiques que l’on apprend aux élèves de lycée, qui parfois se demandent ce qu’elles peuvent bien apporter dans la vie quotidienne. C’est une question légitime : en premier lieu, soyons honnêtes, cela sert surtout à avoir son bac et à pouvoir continuer allègrement dans les études supérieures. Mais concrètement, quelle est l’utilité des logarithmes ?

Pour comprendre que les logarithmes ont eu des applications concrètes dès leur création, nous allons nous pencher sur l’histoire de leur construction. Un nom en particulier reste de cet épisode : Neper et le logarithme Népérien. Comme la géométrie Euclidienne inventée par Euclide, la description Eulérienne inventée par Euler, le logarithme Népérien a été inventé par… Neper ? En fait non, enfin si, mais pas exactement. Neper, écrit en réalité John Napier dans son pays d’origine, l’Écosse, n’a pas inventé le logarithme Népérien tel qu’on l’entend au sens de fonction aujourd’hui. Mais son invention a bien été une étape marquante dans l’histoire des sciences.

John Napier en 1616

Un contexte particulier

Au début du 17^ème siècle, les mathématiciens cherchent des méthodes pour effectuer des calculs plus rapidement. Les besoins de ce siècle en calculs vont en grandissant parce que plusieurs disciplines se développent, et en particulier l’astronomie et la navigation. Si vous voulez aujourd’hui par exemple multiplier la masse de la Lune par la masse de la Terre, vous allez probablement rapidement sortir votre calculatrice. Avant cette invention, les moyens étaient bien moins puissants : il fallait se servir de tables de calculs, et être très vigilant sur les erreurs. Tout cela était fastidieux et il valait mieux ne pas se tromper sous peine de tout recommencer.

Napier est un contemporain de trois astronomes célèbres, Johannes Kepler, Galilée et Tycho Brahe. C’est un siècle révolutionnaire pour l’astronomie, où des scientifiques se battent pour démontrer que la Terre tourne autour du Soleil : c’est la théorie de l’héliocentrisme, qui était une position difficile à défendre. La théorie concurrente, le géocentrisme, où la Terre est le centre de l’univers, est alors dominante.

Pour ces astronomes, l’observation des astres va de pair avec le calcul de leur position, qui se révèle compliqué. De plus, l’astronomie progresse en même temps que la navigation, parce que les marins avaient besoin d’une bonne connaissance du ciel pour s’orienter.

Exemple de système géocentrique, tableau de 1660

Ces travaux scientifiques demandent donc de plus en plus de calculs, mais ils ne sont pas les seuls : avec la navigation se développe aussi le commerce, la circulation de capitaux, et donc les calculs d’intérêts pour des sommes de plus en plus importantes. Par exemple, plus concrètement, en 1494 à Venise, le mathématicien Pacioli se pose la question « combien d’années faut-il pour doubler un capital lorsqu’il est placé à 10% d’intérêts composés ? ». Pour résoudre cette question, il faut savoir résoudre cette équation :

Dans cette équation, l’inconnue à l’exposant est un obstacle de taille parce que les outils mathématiques n’apportaient pas de résolution directe de l’équation. Le problème était contourné généralement avec la création de tables, par exemple à Lyon en 1571, un professeur de mathématiques, Jean Trenchant, créé des tables à partir d’approximations pour ce type de calculs

L’Arithmétique de Jean Trenchant, publié en 1571

Ce contexte fait que l’idée de Neper a connu un grand succès et a été diffusée largement. Elle répond à une problématique importante des mathématiques, qui avait déjà posé problème à Archimède : la multiplication de grands nombres.  Grands comment ? Archimède voulait alors estimer le nombre de grains de sable qu’il faudrait pour remplir l’univers. Le genre de question que tout le monde se pose en somme.

L’idée de Neper

En 1594, Neper était déjà en train de travailler sur ses tables logarithmiques, dont le but était de simplifier les calculs. Il publia son œuvre en 1614.

Le principe était connu : il s’agissait de faire des correspondances entre une suite géométrique – on obtient le terme au rang  en multipliant le terme de rang n-1 par un nombre appelé « raison » – et une suite arithmétique – le terme de rang  est obtenu en additionnant la « raison » au terme de rang n-1. Par exemple : 1, 2, 4, 8 est une suite géométrique de raison 2, et 1, 3, 5, 7 est une suite arithmétique de raison 2.

Exemple de suites arithmétique et géométrique, pour une même raison de 1.2

Quel est le but de Neper ? Remplacer le produit par une somme, ce qui n’est pas rien pour des grands nombres. Pour multiplier deux grands nombres, il suffira de connaître leurs logarithmes respectifs, d’additionner ces logarithmes, puis de retrouver l’antilogarithme de ce résultat dans les tables. Le temps qu’on peut gagner en réalisant une addition à la main plutôt qu’une multiplication, et faire potentiellement des économies sur les salaires des calculateurs, est considérable.

Comment Neper a-t-il établi cette correspondance ?

C’est là que se situe le génie de ces tables, car elles sont non seulement révolutionnaires pour l’outil puissant qu’elles constituent, mais aussi révolutionnaires dans la manière dont elles ont été créées. En premier lieu Neper construit 2 suites : une géométrique et une arithmétique. La suite géométrique est définie sur un segment, où chaque nouveau point est séparé du précédent par une distance plus petite : c’est la distance précédente multipliée par la raison, qui est inférieure à 1.

Suite Géométrique sur un segment

La suite arithmétique est définie sur une droite : chaque nouveau point est séparé du précédent par une distance égale. Cette droite peut continuer indéfiniment, contrairement au segment précédent.

A partir de là toute la « magie » du logarithme va être de trouver la transformation qui lie la longueur AB à αβ, puis BC à αγ, puis CD à αδ, etc. Neper définit cette transformation comme le logarithme (log) :

Suite Arithmétique sur une demi-droite

Le logarithme tient-il ses promesses ?

Prenons un exemple : imaginons que αβ = βγ = γδ = a. De l’autre côté, imaginons qu’on multiplie OA par 0.8 pour avoir AB, puis AB par 0.8 pour avoir BC, etc.

On a donc CD = 0.8 x 0.8 x 0.8 x OA = 0.8³ x OA. Sur l’autre suite, on a αδ = 3 x a.

Donc log (CD) = log (0.8³ x OA) = 3 x a.

Résultat : la fonction tient bien ses promesses ! L’opération puissance de 3 a été transformée en multiplication par 3.

La construction des tables

Pour calculer le premier logarithme, Neper reprend ces schémas et étudie le mouvement de 2 mobiles : l’un se déplaçant sur le segment, dont la vitesse serait proportionnelle à la distance qu’il lui reste à parcourir. Autrement dit, sa vitesse diminue d’autant plus qu’il atteint le bout du segment. L’autre mobile se déplace à vitesse constante sur la droite.

Mais en 1614 la vitesse n’était pas une grandeur mesurable : on considérait son intensité qualitativement, comme on peut le faire pour la couleur. De plus, les variables utilisées étaient des variables discrètes, alors que Neper, dans sa définition, postule la continuité du mouvement : le mobile parcourt tous les points du segment. En utilisant ces notions de vitesses et de continuité, Neper propose une mécanique innovante qui va au-delà des outils de son époque.

Nous allons prendre un exemple simple pour comprendre le principe de son calcul : le but de Neper est de calculer la distance αβ, à partir de AB, en ayant choisi astucieusement la suite géométrique. Imaginons 2 coureurs aux doux noms de C1 et C2. C1 se déplace de α à β à 10 km/h sans ralentir. C2 part en avance, au point O, en ralentissant constamment. Il atteint la vitesse de 10 km/h en A. C2 va donc plus vite que C1 de O à A, et moins vite de A à B. Sachant qu’on choisit que la durée de parcours entre 2 points est toujours la même, la distance OA est donc plus grande que αβ, et AB plus petite.

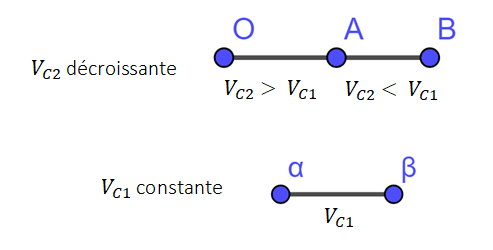
On en déduit : OA > αβ > AB. La valeur αβ est donc encadrée. Alors, par exemple, si OA vaut 1 km et AB 0.8 km, on peut approximer que αβ = 0.9 km.

La valeur αβ dépendra donc de la construction de la suite géométrique, mais en la construisant intelligemment et en ayant des points suffisamment proches, Neper est arrivé à une approximation très proche des valeurs attendues.

Épilogue

Dès 1614, un mathématicien anglais, Henry Briggs, se penche sur ses tables et propose des améliorations. Il publie ses tables en 1617, l’année de la mort de Neper. Briggs va contribuer à rendre ces tables plus populaires auprès des scientifiques, et à les pérenniser. En 1795, le célèbre mathématicien Pierre Simon de Laplace, déclare, à propos des logarithmes : « admirable instrument, qui, en réduisant à quelques heures le travail de plusieurs mois, double si l’on peut dire la vie des astronomes, et leur épargne les erreurs et les dégoûts inséparables des longs calculs ».

Quant au célèbre logarithme Népérien, il a été créé en 1647, 30 ans après la mort de Neper, pour calculer l’aire sous la courbe d’une hyperbole. Une fonction appelée au départ logarithme naturel permettait ce calcul, et, plus tard, le lien a été fait avec les tables de Neper. La fonction a été appelée logarithme népérien en hommage à ce dernier. Bien que Neper soit connu pour les mathématiques, ce n’était pas son activité principale. Les tables logarithmiques sont l’œuvre de la fin de sa vie, mais il était plus connu auparavant en tant que théologien. Il avait notamment prédit la fin du monde à partir de l’Apocalypse, qui devait selon lui arriver soit en 1688 soit en 1700. C’était son petit côté savant fou.

Sources :

Articles sur l’histoire des logarithmes et John Napier sur Wikipédia : https://fr.wikipedia.org/wiki/Histoire_des_logarithmes_et_des_exponentielles et https://fr.wikipedia.org/wiki/John_Napier

Ouvrage sur l’œuvre de Neper : The construction of the wonderful canon of logarithms, sur US archive, par William Rae Macdonald : https://ia800500.us.archive.org/32/items/constructionofwo00napiuoft/constructionofwo00napiuoft_bw.pdf

Livre plus complet sur l’histoire des mathématiques à cette époque : Histoires de Logarithmes, de l’Institut de recherche sur l’enseignement des mathématiques, 2006

Les images sont sous licence Creative Commons.

Image bannière : George M. Groutas via Flicker